Una delle questione più discusse e meno comprese dai non addetti ai lavori è la, cosiddetta, linearità dei sensori d'immagine elettronici.
CCD e CMOS per imaging dovrebbero possedere una una caratteristica fondamentale se si vuole utilizzarli per usi scientifici o anche solo per l'imaging astronomico evoluto: la risposta del sensore alla luce deve essere lineare.
Linearità di risposta significa che l'output del sensore è correlato linearmente con l'intensità della radiazione che lo colpisce.
Se indichiamo con
ADU l'intensità letta sull'immagine uscita dal sensore
I l'intensità della radiazione
t il tempo di posa
K è una costante di proporzionalità fissa, dipendente dalle caratteristiche tecniche del sensore (principalmente efficienza quantica e guadagno).
allora, per un'immagine calibrata con il relativo dark frame, vale la relazione
ADU=K*I*t
Quindi, in un sensore ideale, se raddoppia l'intensità della sorgente luminosa oppure il tempo di posa, allora raddoppia anche il valore di ADU ottenuto sull'immagine finale.
Tale caratteristica è fondamentale in fotometria, dove è assolutamente necessaria per assicurare un'accurata misura delle magnitudini, ma è importantissima anche in fotografia astronomica.
Infatti l'applicazione del flat field, utilizzato per correggere i difetti moltiplicativi introdotti dall'ottica (vignettatura, polvere, variazioni di efficienza quantica), presuppone che il sensore sia lineare: se non lo è la calibrazione è destinata a fallire.
Quindi se si desidera utilizzare il proprio sensore per fotometria, oppure se si hanno problemi nell'applicazione di correzione per il flat field, diventa necessario verificare l'effettiva linearità del sensore.
Il modo migliore per effettuare questa analisi è esporre il sensore ad intensità note di radiazione, per un tempo definito e leggere il relativo valore di ADU dopo la calibrazione.
Purtroppo, soprattutto a livello amatoriale, è molto difficile ottenere una sorgente luminosa perfettamente controllabile, quindi si utilizza un metodo alternativo: al posto di far variare l'intensità I, nell'equazione sopra si fa variare t, assumendo che il controllo dei tempi di esposizione sia preciso ed accurato.
Il metodo è descritto molto bene nell'articolo di Danele Gasparri che potete leggere sul sito di Teleskop-Express.
Rispetto al metodo descritto da Daniele, applico tre varianti:
Al posto di utilizzare i residui assoluti, dati dalla differenza tra il valore calcolato tramite regressione lineare e quello effettivamente misurato, utilizzo quelli relativi (differenze percentuali), ossia il residuo assoluto diviso per il valore in ADU del punto a cui si riferisce.
Questo è, infatti, un valore più significativo rispetto alla deviazione assoluta dalla linearità: se a 100 ADU ho un residuo di 2 ADU e a 30.000 ADU ne ho uno di 300, utilizzando i residui assoluti, sembrerà che il sensore a 30.000 ADU sia molto peggiore che a 100, in realtà a 100 ADU la deviazione è del 2% (2/100) mentre a 30.000 ADU è dell'1% (300/30.000) quindi molto inferiore di quella a 100.
La seconda modifica è che, effettuando diverse misure per ogni tempo di posa, oltre a calcolare la media calcolo anche la loro deviazione standard.
La deviazione standard, infatti, permette di valutare l'incertezza di misura: una misura senza l'incertezza ad essa associata è difficilmente interpretabile.
Infine, come ultima modifica, nel grafico dei residui, utilizzo il valore di ADU al posto del tempo di posa come asse delle ascisse: in questo modo è possibile identificare facilmente a che livello di esposizione (in ADU) avvengono eventuali fenomeni di non linearità ed inoltre diventa possibile confrontare, sul medesimo grafico, dati acquisiti in sessioni diverse, con diverse luminosità della sorgente.
Ho provato quindi ad applicare questo metodo così modificato alla mia Moravian G3 16200, un CCD che non dovrebbe avere problemi di linearità su buona parte del suo range dinamico.
Questi i dati grezzi
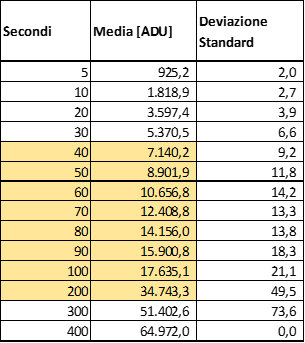
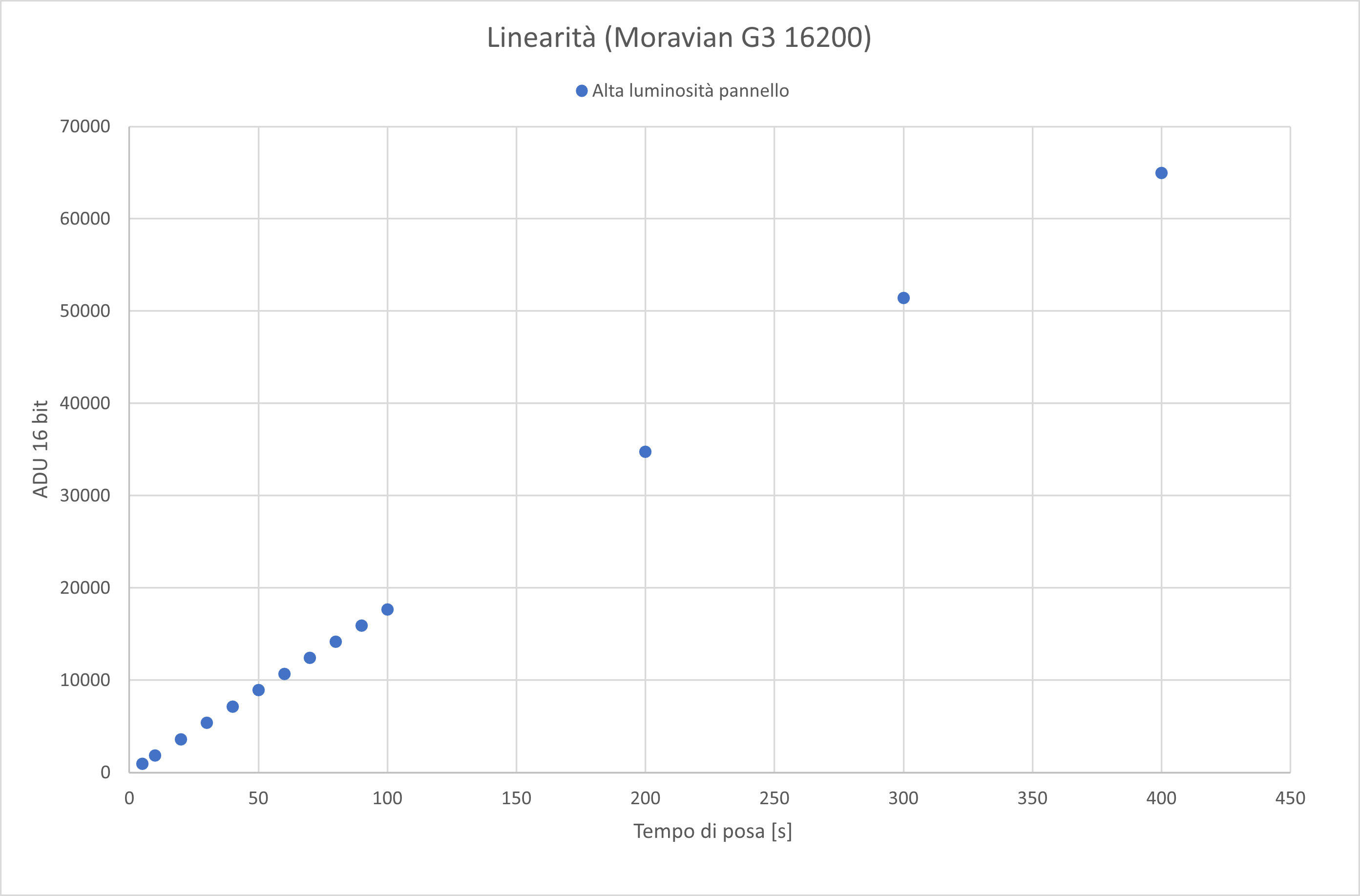
e questo il relativo grafico di linearità.
Volendo si può aggiungere una seconda serie di dati diminuendo l'intensità della fonte luminosa in modo da "esplorare" valori di ADU più bassi.
Mantenendo gli stessi tempi di posa per la seconda serie e aggiungendo le rette di regressione lineare si ottiene il seguente grafico.
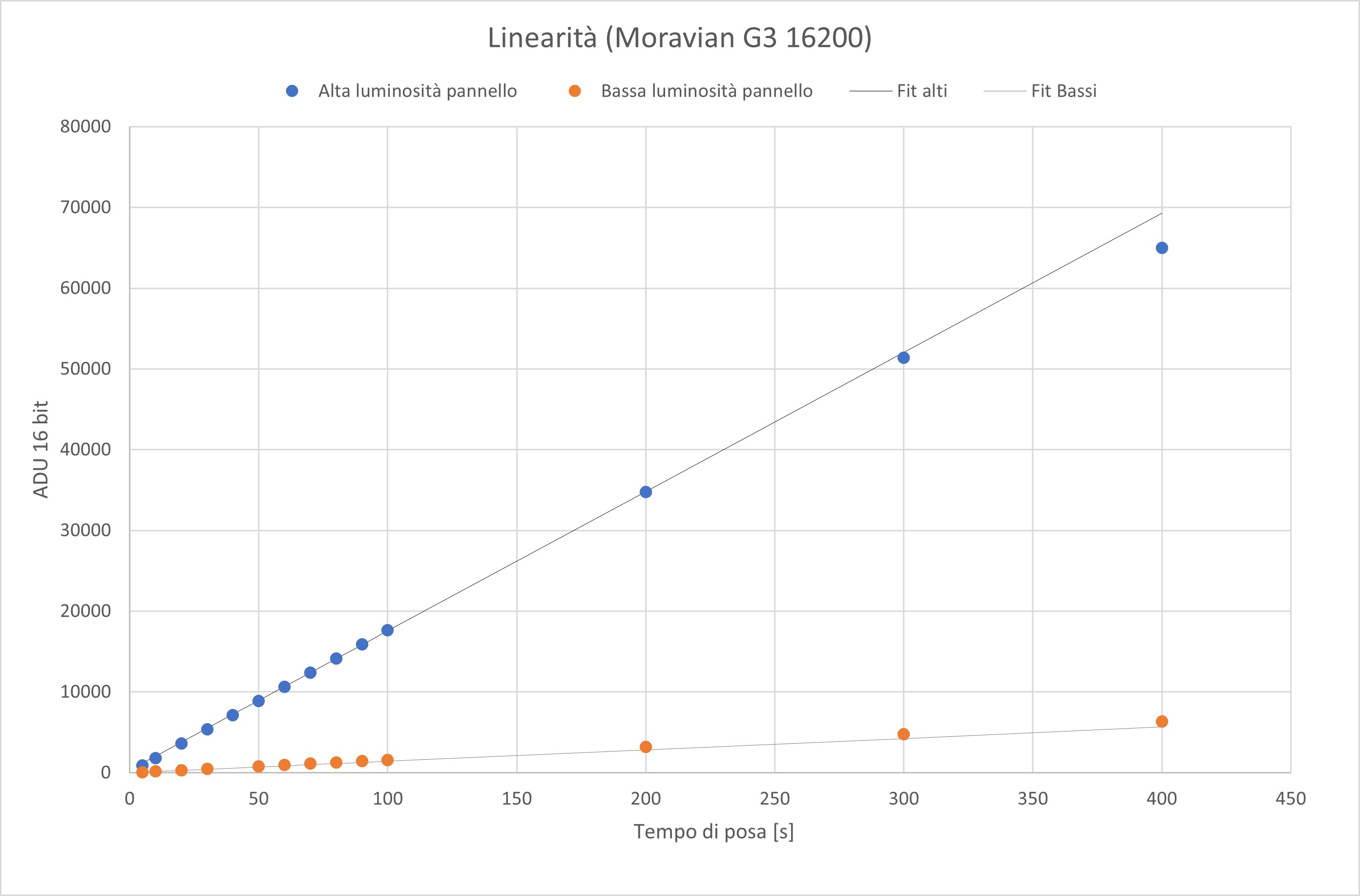
Ad un primo sguardo sembrerebbero non esserci problemi, si nota una leggera inflessione dell'ultimo punto dei dati ad "alta luminosità" dovuta alla saturazione del sensore, ma in generale sembra comportarsi bene.
Quando però si vanno ad analizzare i residui arrivano le sorprese.
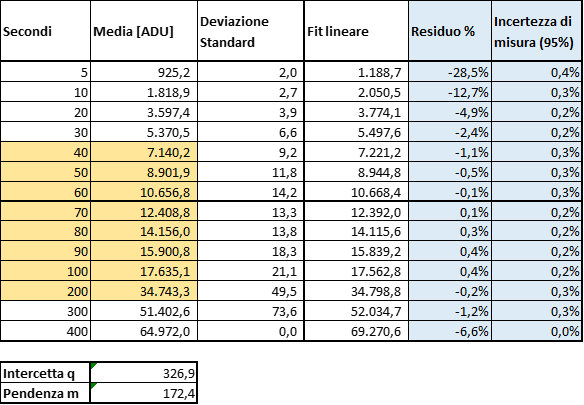
A titolo di esempio questi sono i dati ad alti ADU (i dati evidenziati in arancio sono quelli utilizzati per la regressione lineare)
e questo il grafico dei residui di due set di dati con due livelli di luminosità diversi (e barre di errore al 95% di confidenza).
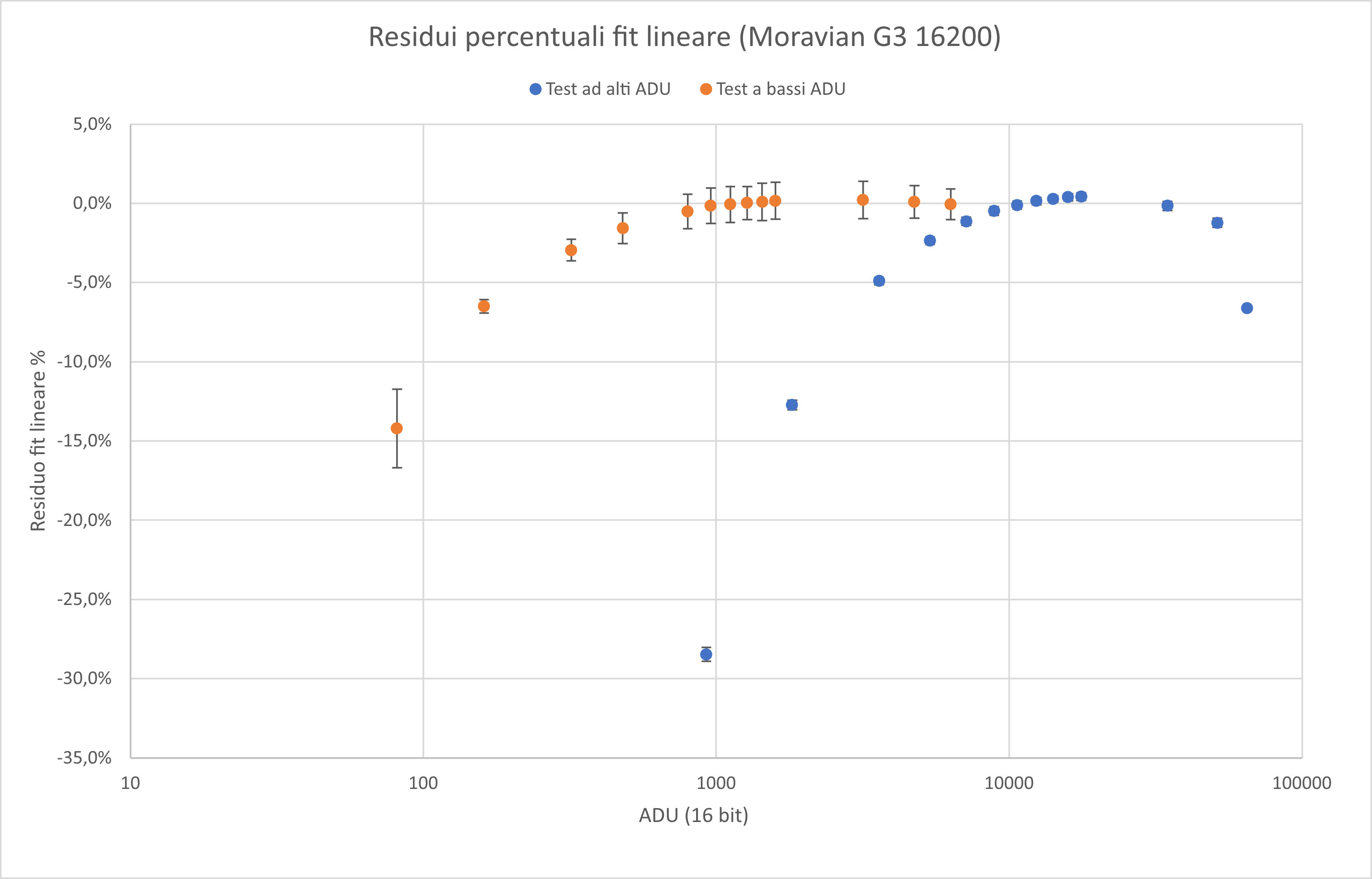
Che cosa è andato storto?
Non solo il sensore della Moravian 16200 sembrerebbe non lineare (con differenze ai bassi ADU che sfiorano il 30%) ma sembra avere un comportamento erratico dipendente dalla luminosità del pannello utilizzato per illuminare il sensore: infatti, se anche il sensore avesse una pronunciata non linearià ai bassi ADU, nelle zone di sovrapposizione dei due set di dati, tra i 1000 e i 10000, dovrebbe comportarsi nello stesso modo (i punti blu e arancio dovrebbero sovrapporsi entro le barre di errore).
Un sensore del genere sarebbe totalmente inutilizzabile per la fotografia astronomica (oltre che incomprensibile la punto di vista fisico).
Dal momento che utilizzo questa camera senza grossi guai di calibrazione, il problema deve risedere nel metodo di misura e non nello strumento.
La soluzione al mistero arriva dalla verifica dei presupposti alla base di questo tipo di analisi.
Le condizioni sono:
- L'intensità della fonte luminosa deve essere costante durante tutta l'esecuzione della prova
- Il tempo di posa impostato dal software deve essere rigorosamente riprodotto dalla camera
Se uno di queste due condizioni viene a mancare allora l'esperimento è destinato a fallire: in questo caso l'anello debole è proprio nell'accuratezza del tempo di posa..
La Moravian G3 16200 ha un otturatore meccanico a pala rotante, questo tipo di otturatore impiega un tempo non trascurabile per aprirsi e chiudersi: ciò significa che il sensore viene tipicamente esposto per un tempo inferiore a quello "nominale".
Dal momento che, qualunque sia il tempo di posa nominale, il "tempo di transito" della paletta dell'otturatore è sempre lo stesso, questo effetto è tanto più importante quanto più breve è il tempo di posa, andando a minare alle fondamenta il test di linearità basato sui residui.
Ecco il motivo per cui i due grafici dei residui non si sovrappongono: per tempi di posa inferiori a 60- secondi i dati sono affetti da un significativo errore sistematico.
Per minimimizzare tale errore, è necessario usare tempi di posa superiori a 60 secondi, il che significa dover usare sorgenti luminose molto deboli.
Tali sorgenti però rischiano di diventare instabili e far cadere la condizione 1 riportandoci di nuovo nell'incertezza inoltre i tempi di esecuzione della prova che esploderebbero rapidamente.
Si rende quindi necessario sviluppare un metodo che possa risultare indipendente dal tempo di posa.
Il metodo del gradiente locale
L'equazione di linearità scritta all'inizio dell'articolo è valida solo se il sensore viene colpito da una radiazione incidente perfettamente uniforme su tutti i pixel.
In pratica però questo non avviene mai: qualunque sistema ottico è affetto da "difetti" che riducono tale intensità in modo disomogeneo sulla superficie del sensore.
Vignettatura e granelli di polvere, producono una illuminazione non omogenea del sensore: Il metodo del gradiente locale utilizza proprio questo effetto.
Il trucco consiste nel produrre un'immagine affetta da una forte vignettatura in modo che il sensore venga illuminato in maniera non omogenea.
indichiamo con Gp la "mappa" della vignettatura.
Tale funzione mi dice come varia l'intensità della vignettatura al variare della posizione sul sensore, pertanto l'equazione di linearità diventa
ADU=K*I*Gp*t
Si misura quindi il valore di ADU in due diverse regioni sull'immagine: una vicina al centro, dove il segnale sarà maggiore (ADUc), e una vicina al bordo dell'immagine, dove il segnale sarà minore (ADUb).
Il gradiente locale LG(adu) è definito come il rapporto tra questi due valori.
In generale tale valore potrebbe dipendere dal valore di ADU, ma, se in sensore è lineare, si può applicare l'equazione sopra e quindi
LG(adu)=ADUc/ADUb = (K*I*Gc*t)/(K*I*Gp*t)
Come si può vedere, nel rapporto sopra, K, I e, soprattutto, t si semplificano (essendo un'unica immagine, sia il tempo di posa che l'intensità della sorgente sono gli stessi) quindi.
LG=Gc/Gp
Si giunge quindi alla notevole osservazione che, se il sensore è lineare, il gradiente locale è indipendente dalle caratteristiche del sensore (K), dalla luminosità della sorgente di luce (I) e, soprattutto, da tempo di posa (t) e quindi indipendente dagli ADU: dipende esclusivamente dalla "geometria" della vignettatura.
Ossia, in parole povere, se il sensore è lineare il rapporto LG avrà lo stesso valore qualunque sia la luminosità dell'immagine utilizzata per il calcolo del rapporto.
ATTENZIONE: la linearità del sensore è condizione sufficiente affinchè il gradiente locale sia constante, ma non è necessaria (esistono altre funzioni dell'intensità che potrebbero produrre un rapporto costante), pertanto il metodo del gradiente locale non può sostituire totalmente il metodo della regressione linare, ma solo integrarne i risultati.
Un'analisi completa di un sensore CCD, quindi, dovrebbe comprendere entrambi i test.
Il metodo operativo
Il metodo di acquisizione è simile a quello utilizzato per il test di linearità con il metodo dei residui.
Al posto di illuminare tutto il sensore in maniera omogenea, però, cerco di produrre una forte vignettatura.
Nel mio caso ho utilizzato un tappo filettato con un piccolo buco al centro, in modo da produrre un'illuminazione intensa al centro con un gradiente di luminostià piuttosto prinunciato verso i bordi.
Ho quindi appoggiato il sensore su una flatbox in modo da avere una fonte di illuminazione costante.
Ho quindi esposto il sensore, utilizzando il filtro Hα per attenuare ulteriormente la sorgente, per tempi variabili tra 5 e 400 secondi.
Questo mi ha permesso di ottenere valori ADU circa tra 80 e 6000.
Quindi ho aumentato la luminosità del pannello e ripetuto la sequenza ottenendo valori da 1000 ADU fino alla saturazione del sensore.
per ogni combinazione tempo-luminsità ho aquisito 5 immagini in modo da avere una migliore statistica e stimare l'errore sperimentale.
Inoltre, per ogni tempo di posa ho acquisito 10 dark frame in modo da poter calibrare ogni immagine con il proprio dark.
Questa è una condizione NECESSARIA affichè il metodo dei rapporti funzioni, infatti è necessario rimuovere dall'immagine ogni contributo additivo, mantenendo solo quelli moltiplicativi descritti dall'equazione di linearità..
Nell'immagine sotto si vede uno di questi light frame calibrati utilizzati per il test.

L'estrazione dei dati è stata eseguita grazie a PixInsight: è infatti importantissimo valutare il rapporto esattamente nelle stesse posizioni in tutte le immagini.
Ultilizzando il process DynamicCrop ho definito due regioni da 100x100 pixel, una al centro esatto dell'immagine, l'altra vicino al bordo superiore e, utilizzandone le icone di processo, ho estratto due set di immagini:
la serie C (centro) e la serie B (Bordo).
Grazie allo script BachStatistics ho misurato, per ciascun "ritaglio" il valore mediano, salvando il dato in un file CSV.
I due file sono stati poi importati in Excel e, grazie ad una banale tabella pivot, sono state ottenute le tabelle indicanti, per ogni tempo di posa, il valore medio e la deviazione standard del campione.
N.B. PixInsight gestisce valori normalizzati (tra 0 e 1) pertanto, per ottenere una rappresentazione in ADU, più comprensibile per la maggior parte degli astrofili, è bastato moltiplicare per 65535 (dato che il sensore è a 16 bit)
Grazie a tali dati è stato infine possibile ottenere la tabella che segue:
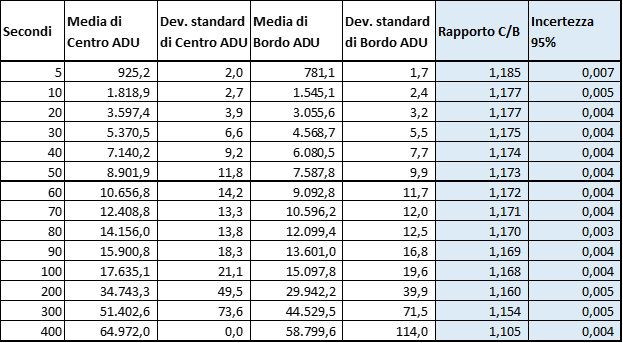
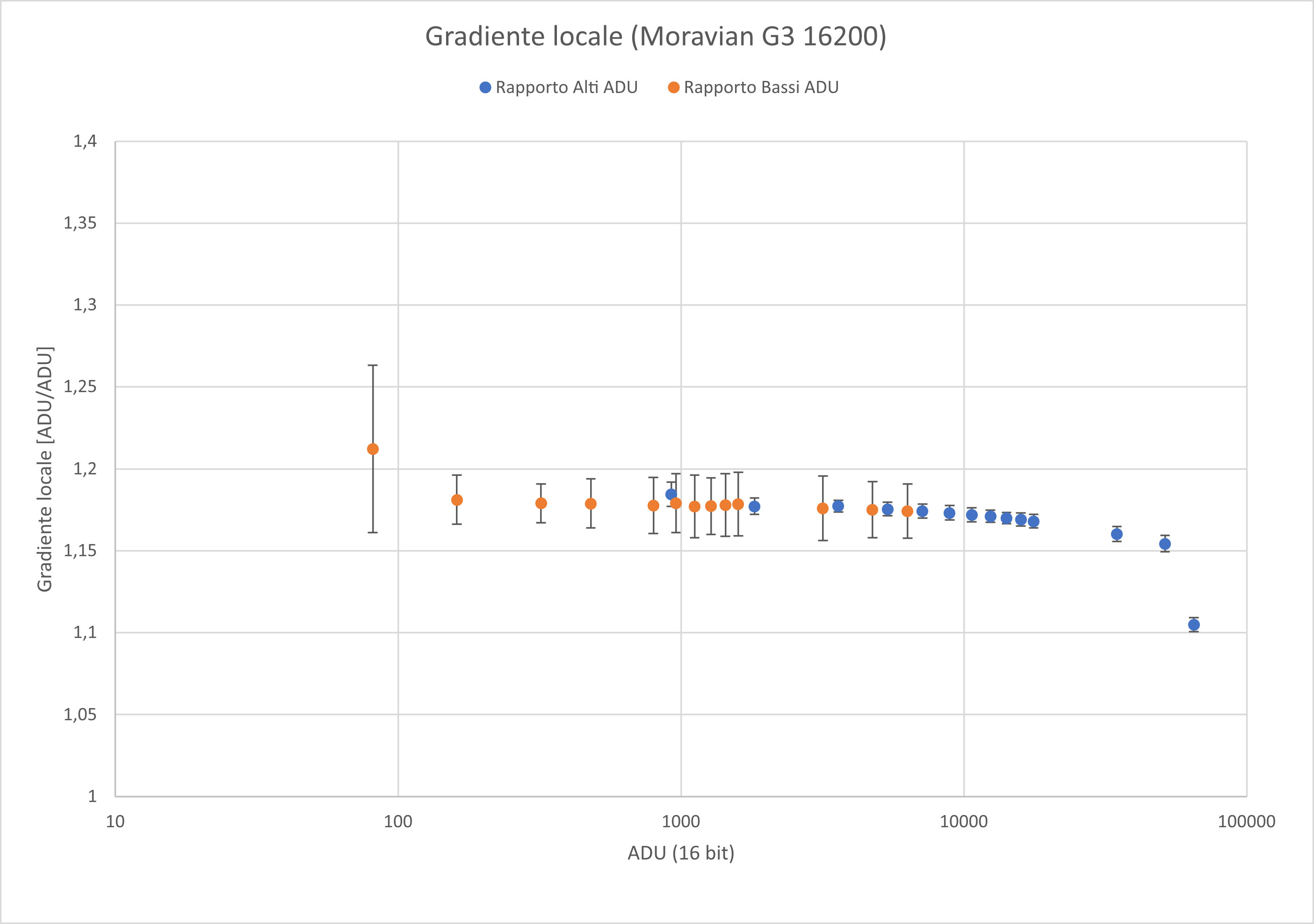
e il relativo grafico dei rapporti.
L'interpretazione dei dati
Bene, è venuto il momento di interpretare i dati in nostro possesso: per comodità riporto qui il grafico dei residui da confrontare con quello dei gradienti locali riporato poco sopra

Ricordiamo alcuni punti fondamentali utili ad interpretare questi test:
- Tutti i grafici sono esposti utilizzando gli ADU Del centro immagine come variabile indipendente: questo permette di confrontare dati presi in condizioni di illuminazione diversa.
- L'asse degli ADU è rappresentato in forma logaritmica per separare meglio i dati a bassi ADU.
- I tempi di posa della serie ad alti ADU sono 5s, 10s, 20s, 30s, 40s, 50s, 60s, 70s, 80s, 90s, 100s, 200s, 300s, 400s
- I tempi di posa della serie a bassi ADU sono gli stessi della serie ad alti ADU salvo per il punto a 40 secondi che manca a causa di un inconveniente tecnico.
- I residui sono esposti come residuo relativo, ossia normalizzato sul rispettivo valore ADU, questo consente un'effettiva valutazione dell'entità della deviazione dalla linearità
- Nel grafico dei residui, più un valore è vicino allo zero e migliore è la linearità del sensore in quella zona.
Fatte queste premesse come possono essere interpretati i dati?
Il grafico dei residui ci dice che, almeno su una pare del range dinamico, il sensore è perfettamente lineare (tra i 1.000 e i 40.000 ADU), osservando il grafico del gradiente locale si nota che, anche sotto tale valore il sensore rimane perfettamente lineare, infatti il rapporto rimane costante.
L'apparente deviazione dalla linearità è quindi spiegabile con un problema di accuratezza nei tempi di posa: l'otturatore meccanico della Moravian è decisamente poco affidabile, ma questo ovviamente non costituisce alcun problema per la fotografia astronomica.
Agli alti ADU si nota una leggera flessione sia nel grafico dei residui che in quello del gradiente locale.
Trale flessione è imputabile all'entrata in funzione della barriera antiblooming tipica delle camere pensate per la fotografia astronomica di tipo "estetico".
Tale inflessione è comunque molto contenuta fino a circa 40.000 ADU dove si attesta intorno all'1% (questa sarebbe l'entità di un eventuale errore sistematico nelle misure di magnitudine se si dovesse raggiungere il limite di 40.000 ADU).
Oltre i 50.000 ADU la deviazione diventa infine sempre più pronunciata fino a sfociare nella satuazione del sensore dove si ha la perdita definitiva della linearità.
Infine, nel grafico dei gradienti locali, il primo punto di entrambe le serie (5 secondi di esposizione) sembra sensibilmente più altro rispetto agli altri (sebbene sia ancora compatibile entro l'errore sperimentale)
Questo è un ulteriore effetto dovuto all'otturatore rotante: non solo il tempo di posa è notevolmente inferiore a quello nominale, ma il sensore risulta esposto in maniera non omogenea.
La porzione di sensore più vicina al centro di rotazione dell'otturatore resta "in ombra" per un tempo maggiore rispetto alla porzione più lontana, quindi sul sensore si forma un gradiente di luminosità che produce un'apparente non linearità.
Questo porta ad una notevole osservazione: quando si aquisiscono le immagini di calibrazione, nel riprendere i flat field, è cosigliabile usare tempi di posa di almeno 10 secondi per evitare che il fenomeno sopra descritto crei dei gradienti fittizi sulle nostre immagini.
In conclusione la Moravian G3 16200, stando a questo test, è un ottimo sensore per astrofotografia, con un ottima linearità nel range tra 50 e 40.000 ADU e con una deviazione marginale fino ai 55.000.
Viste queste caratteristiche può essere utilizzata anche per studi fotometrici, a patto di non avvicinarsi troppo al limite dei 40.000, dove l'intervento della barriera antiblooming produce una sottostima del flusso di oltre l1%.



